\(1\)の原始\(20\)乗根\(\zeta=e^{2\pi i/20}\)に対し、以下の等式が成立する: \[ |1+\zeta^2| = |1+\zeta^3+\zeta^7|. \] この等式を証明すること自体は難しくない。両辺を二乗すれば \[ 2+\zeta^2+\zeta^{18}=3+\zeta^3+\zeta^4+\zeta^7+\zeta^{13}+\zeta^{16}+\zeta^{17} \] を示すことに帰着されるので、あとは\(\zeta\)の最小多項式を使えばよい。 しかしこの証明は、こんな簡潔な等式が一体なぜ存在するのか、という不思議さに対する答えにはならない。
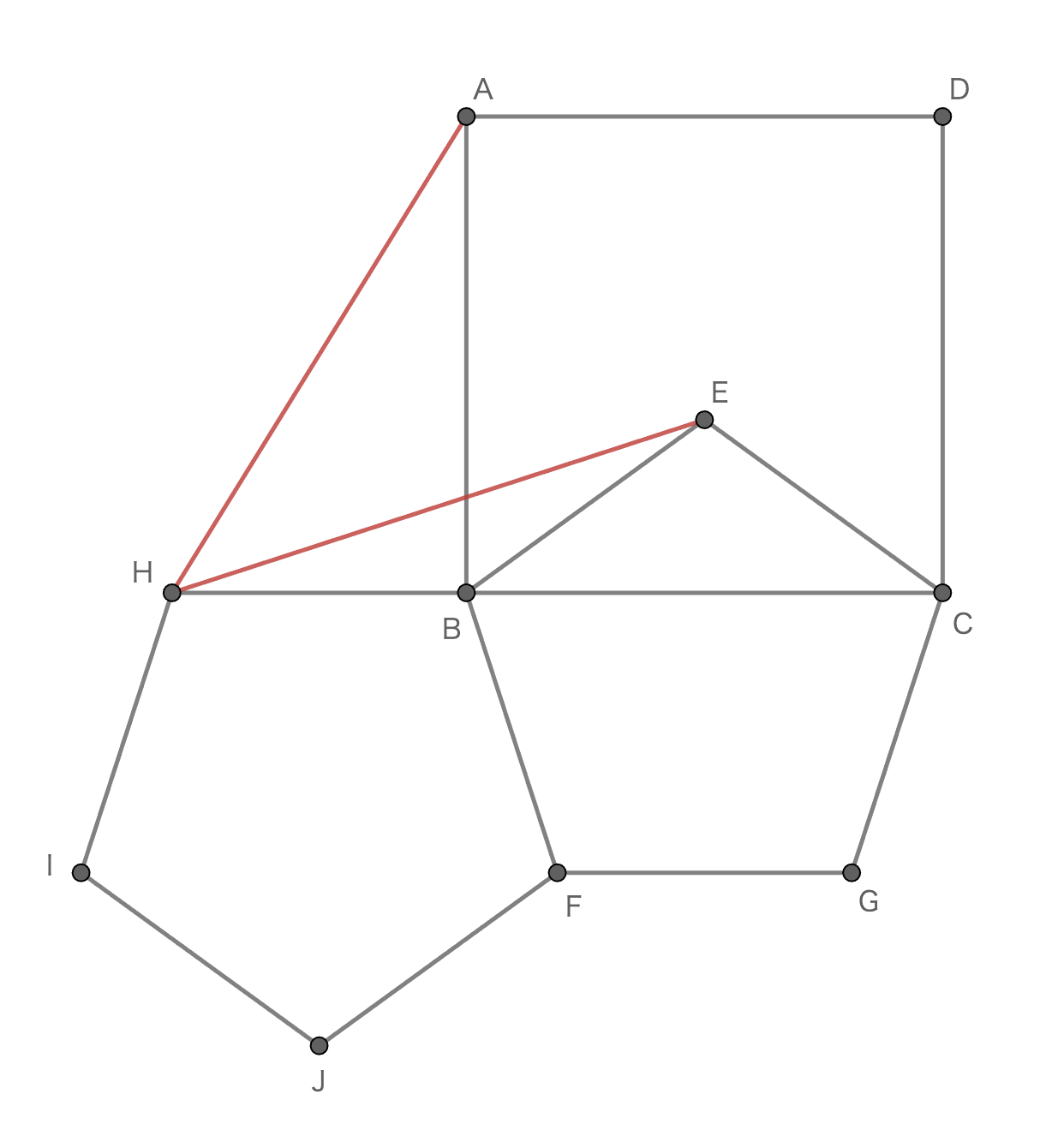
そこで幾何学的な解釈を考えると次のようになる。正五角形と正方形を以下の図のように組み合わせる。このとき \[ AH=EH \] が成り立つ、というのがちょうど最初の等式と同値な主張である。

こうしてみると算数の簡単な問題のように見えるかもしれないが、これを幾何的に証明するのは意外と難しい。 角\(AHE\)はわかりやすい角度(度数法で整数)にならないので、角度計算のみで示すことは不可能である。 いろいろ考えた結果、次のように立体図形を利用する方法を思いついた。
正五角形と正方形が共存する綺麗な図形といえばやはり正十二面体である。 上の図の右側の正五角形を正十二面体の一つの面に貼り付けてみる。 正方形\(ABCD\)を奥に倒していくと、\(A\)と\(D\)がちょうど正十二面体の頂点に重なる。
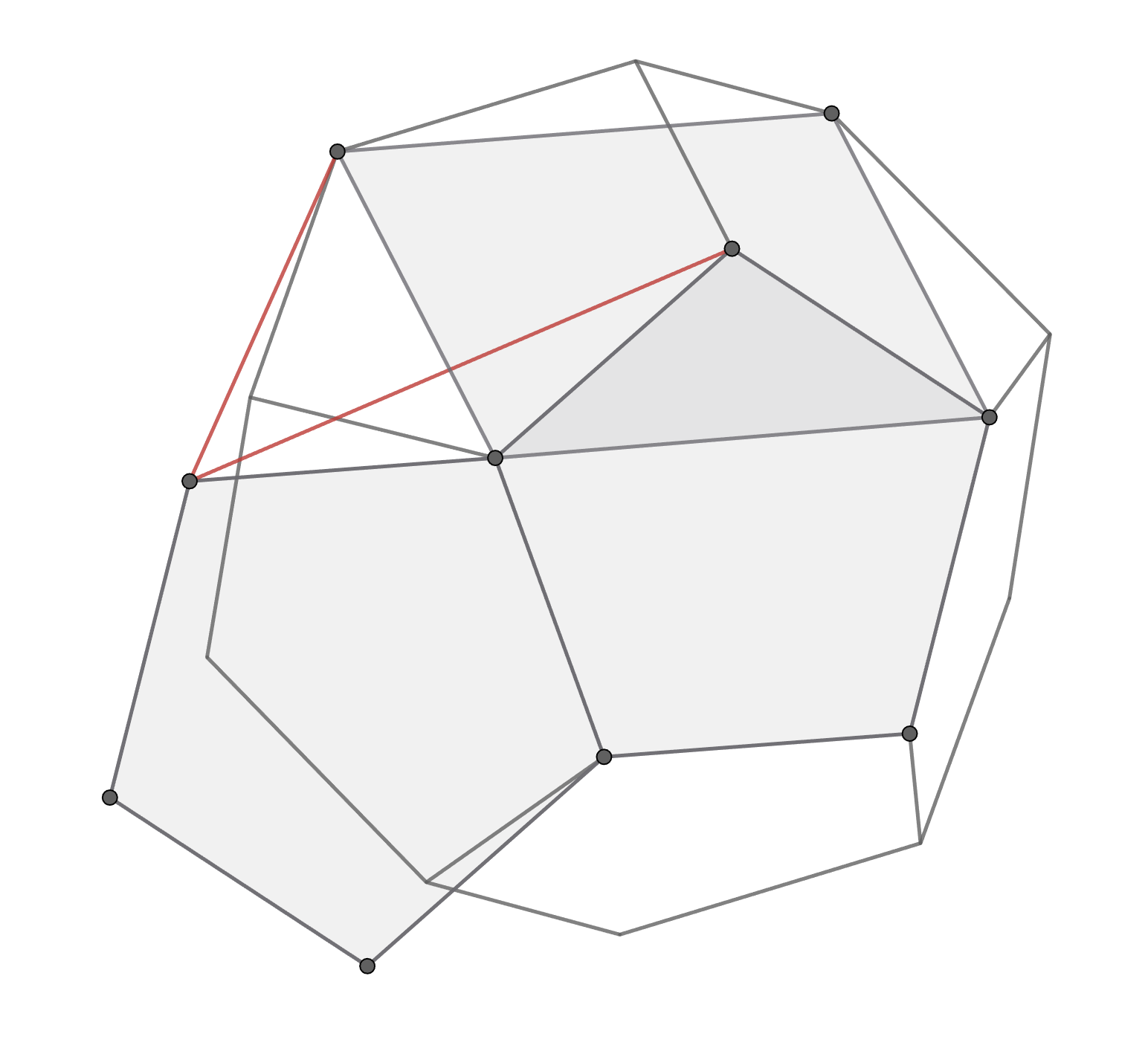
正方形を倒す過程で\(AH\)と\(EH\)の長さは変わらないので、倒したあとに長さが等しいことを示せばよい。 これは正十二面体を上から見れば、対称性から明らかである。
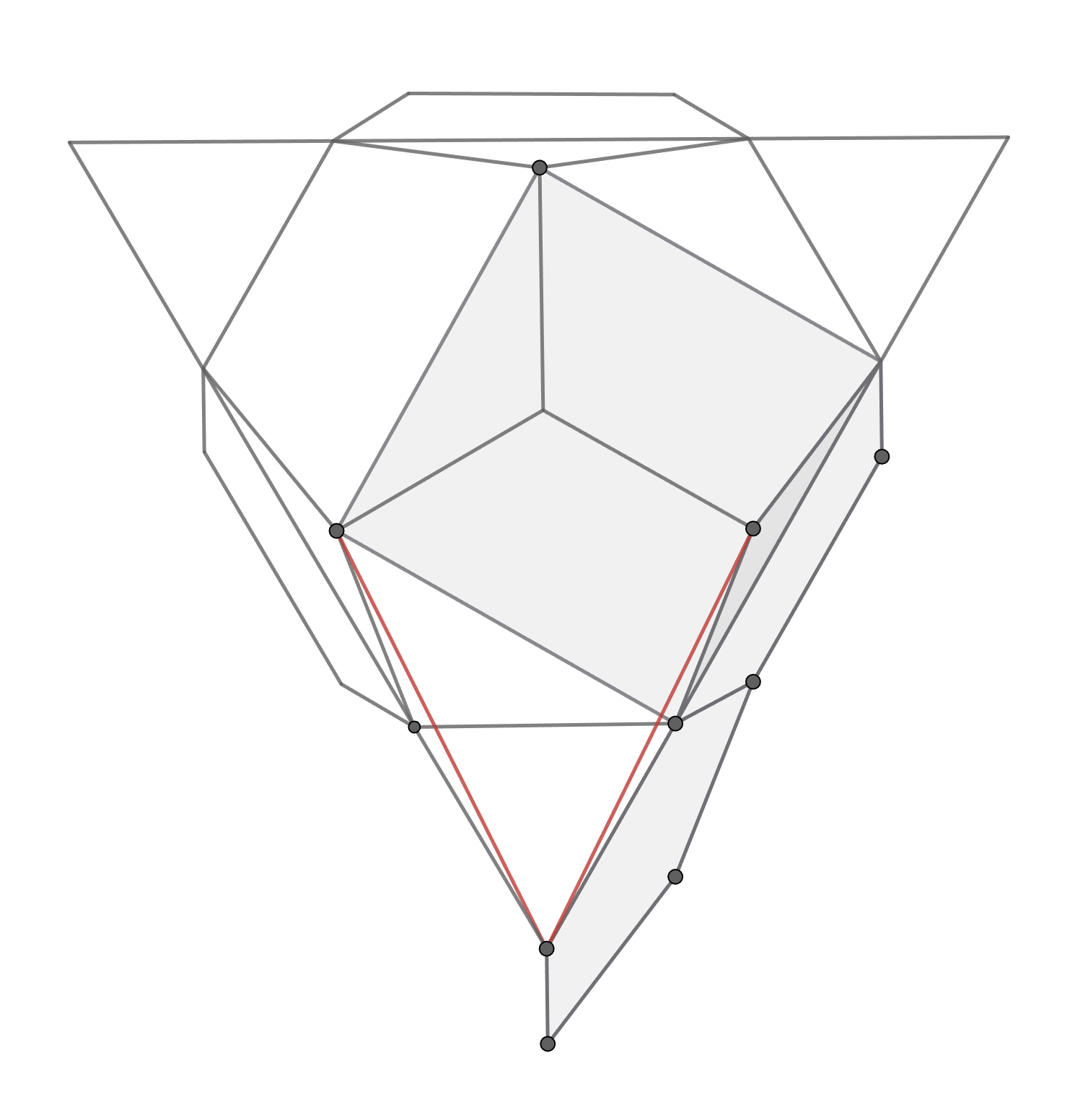
そういうわけで結局、最初の等式は「正十二面体から生じる一つの長さを二通りの方法で計算した結果」だったわけである。
常々思っていることだが、何かを証明することと理解することの間には大きな隔たりがある。 そして、本当に面白いことはしばしば証明のその先にある。